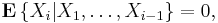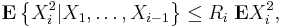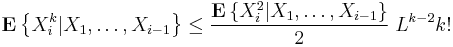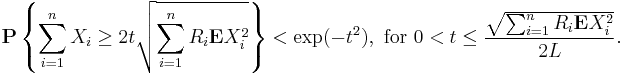Bernstein inequalities (probability theory)
In probability theory, Bernstein inequalities give bounds on the probability that the sum of random variables deviates from its mean. In the simplest case, let X1, ..., Xn be independent Bernoulli random variables taking values +1 and −1 with probability 1/2, then for every positive 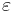 ,
,
Bernstein inequalities were proved and published by Sergei Bernstein in the 1920s and 1930s.[1][2][3][4] Later, these inequalities were rediscovered several times in various forms. Thus, special cases of the Bernstein inequalities are also known as the Chernoff bound, Hoeffding's inequality and Azuma's inequality.
Contents |
Some of the inequalities
1. Let X1, ..., Xn be independent zero-mean random variables. Suppose that |X i| ≤ M almost surely, for all i. Then, for all positive t,
2. Let X1, ..., Xn be independent random variables. Suppose that for some positive real L and every integer k > 1,
Then
3. Let X1, ..., Xn be independent random variables. Suppose that
for all integer k > 3. Denote 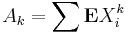 . Then,
. Then,
4. Bernstein also proved generalizations of the inequalities above to weakly dependent random variables. For example, inequality (2) can be extended as follows. Let X1, ..., Xn be possibly non-independent random variables. Suppose that for all integer i > 0,
Then
Proofs
The proofs are based on an application of Markov's inequality to the random variable 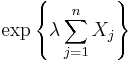 , for a suitable choice of the parameter
, for a suitable choice of the parameter 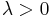 .
.
See also
- McDiarmid's inequality
- Markov inequality
- Hoeffding's inequality
- Chebyshev's inequality
- Azuma's inequality
- Bennett's inequality
References
(according to: S.N.Bernstein, Collected Works, Nauka, 1964)
- ^ S.N.Bernstein, "On a modification of Chebyshev’s inequality and of the error formula of Laplace" vol. 4, #5 (original publication: Ann. Sci. Inst. Sav. Ukraine, Sect. Math. 1, 1924)
- ^ Bernstein, S. N. (1937). "[On certain modifications of Chebyshev's inequality]". Doklady Akademii Nauk SSSR 17 (6): 275–277.
- ^ S.N.Bernstein, "Theory of Probability" (Russian), Moscow, 1927
- ^ J.V.Uspensky, "Introduction to Mathematical Probability", McGraw-Hill Book Company, 1937
A modern translation of some of these results can also be found in M. Hazewinkel (trans.), Encyclopedia of Mathematics, Kluwer, 1987, under the entry "Bernstein inequality" (online version).
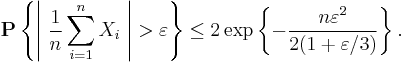
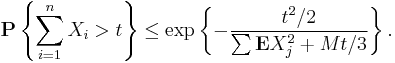
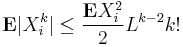
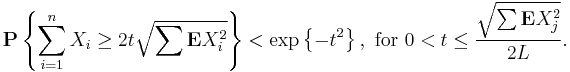
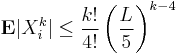
![\mathbf{P} \left\{ \left| \sum_{j=1}^n X_j - \frac{A_3 t^2}{3A_2} \right|
\geq \sqrt{2A_2} \, t \left[ 1 %2B \frac{A_4 t^2}{6 A_2^2} \right] \right\}
< 2 \exp \left\{ - t^2\right\},\text{ for } 0 < t \leq \frac{5 \sqrt{2A_2}}{4L}.](/2012-wikipedia_en_all_nopic_01_2012/I/0585ae2b116d48339cd0f88194d3d4af.png)